FACTORIZACION
CASOS DE FACTORIZACIÓN

CONCEPTOS GENERALES SOBRE LA FACTORIZACIÓN:
¿Qué es factorizar o factorear un
polinomio?
Factorizar o
Factorear significa "transformar en multiplicación" (o "producto",
como también se le llama a la multiplicación). Partimos de una expresión
formada por sumas y/o restas de términos (x2 + 3x + 2 por ejemplo), y llegamos
a una expresión equivalente, pero que es una multiplicación ( (x + 2).(x + 1)
en nuestro ejemplo).
¿Por qué se llama
"factorizar" o factorear?
Porque a los
elementos que están multiplicando en una multiplicación se les llama
"factores". Por ejemplo, en la multiplicación 2 x 3 = 6 , el 2 y el 3
son los "factores".
En el ejemplo
del punto anterior, (x + 2) y (x + 1) son los factores.
¿Para qué sirve factorizar un
polinomio?
Por ejemplo,
tener factorizada la fórmula de una función polinómica sirve para encontrar o
visualizar los "ceros" o "raíces". Y eso es algo de gran
utilidad en varios temas: para analizar la positividad y negatividad de la
función, o para encontrar los máximos y/o mínimos. También la factorización de
polinomios se puede utilizar para: resolver inecuaciones de grado 2 o mayor,
hallar algunos límites, resolver ecuaciones polinómicas fraccionarias,
identidades y ecuaciones trigonométricas, etc. Es decir que nos enseñan a
factorizar porque en otros temas de Matemática necesitaremos factorizar
polinomios para trabajar con multiplicaciones en vez de sumas y restas.
¿Cómo puedo saber si factoricé
correctamente?
Multiplicando
los factores que obtuvimos tenemos que poder llegar a la misma expresión de
sumas y/o restas de la que partimos. No olvidemos que al factorizar estamos
obteniendo una expresión equivalente a la original, pero con distinta forma (de
multiplicación). Si luego multiplico todos los factores que quedaron en el
resultado, tengo que volver "al principio". De esta forma estamos
haciendo una "verificación". Por ejemplo:
Factoreo (con
el Séptimo caso: Trinomio de segundo grado):
x2 + 3x + 2 =
(x + 2).(x + 1)
Verificación
(Multiplicación aplicando la Propiedad distributiva):
(x + 2).(x +
1) = x2 + x + 2x + 2 = x2 + 3x + 2
En casi todos
los casos se puede decir que "factorizar es lo contrario de
multiplicar" o "factorizar es lo contrario de aplicar la
distributiva" (Propiedad distributiva de la multiplicación con la suma).
CASOS:
1) Factor
Común (o "Primer Caso")
2) Factor
Común en Grupos (o "Segundo Caso")
3) Trinomio
Cuadrado Perfecto (o "Tercer Caso")
4)
Cuatrinomio Cubo Perfecto (o "Cuarto Caso")
5) Diferencia
de Cuadrados (o "Quinto Caso")
6) Sumas o
Restas de Potencias de Igual Grado
(o
"Sexto Caso")
7) Trinomio
de Segundo Grado (o "Séptimo Caso")
CASO 1:
FACTOR
COMÚN / EXPLICACIÓN DEL EJEMPLO 1
EJEMPLO 1:
(Hay factor común entre los números)
8a - 4b + 16c
+ 12d = 4. (2a - b + 4c + 3d)
El factor
común es el número 4, el Máximo Común Divisor entre los números.
EXPLICACIÓN:
"Saco"
el número 4 multiplicando a un paréntesis (¿por qué el 4?). A eso se le dice
"sacar factor común 4". Luego divido a cada término por el número 4,
y voy poniendo todos los resultados dentro del paréntesis, sumando o restando
según el signo que resulte de la división. Así:
Primer
término:
8a : 4 =
2a este término dió
"positivo"
Segundo
término:
-4b : 4 =
-b este término dió
"negativo"
Tercer
término:
16c : 4 = 4c
Cuarto
término:
12d : 4 =
3d ( ¿Cómo se hacen
estas divisiones? )
De esa manera
obtuve cada uno de los términos que puse dentro del paréntesis. Sacar factor
común 4 significa "dividir a todos los términos por 4".
Observación:
Al dividir todos los términos por un número positivo, todos los términos
resultaron con el mismo signo que ya traían.
FACTOR COMÚN /
EXPLICACIÓN DEL EJEMPLO 2
EJEMPLO
2: (Hay factor común entre las letras)
El
factor común es x2 , la menor potencia con que la x aparece en el polinomio.
EXPLICACIÓN:
Aquí
estoy sacando factor común x2, porque es la "x" elevada a la menor
potencia con que aparece en este polinomio. Luego divido cada término por x2,
recordando que para dividir las letras hay que restar los exponentes.
(Propiedad
de las potencias de igual base).
FACTOR COMÚN /
EXPLICACIÓN DEL EJEMPLO 3
EJEMPLO 3: (Con fracciones)
El
factor común es 2/3 x: El MCD del numerador sobre el MCD del denominador, y la
x a la menor potencia.
EXPLICACIÓN:
1)
Saco factor común 2/3 x.
¿Por
qué 2/3? Cuando hay fracciones, puedo pensarlo así: Saco el factor común entre
los numeradores por un lado, y saco el factor común de los denominadores por el
otro. El factor común del polinomio será una fracción formada por esos dos
factores comunes, en su respectivo orden.
_____________________________________________________________________
CASO II
FACTOR COMÚN EN GRUPOS /
EXPLICACIÓN DEL EJEMPLO 1
EJEMPLO
1: (Todos los términos son positivos)
4a +
4b + xa
+ xb =
4.(a
+ b) +
x.(a + b) =
(a + b).(4 + x)
EXPLICACIÓN:
Saco
factor común "4" en el primer y segundo término; y factor común
"x" en el tercer y cuarto término. Los dos "resultados" son
iguales: (a + b). Luego, saco como factor común a (a + b).
Nota: Para entender este caso, primero hay
que saber sacar Factor Común, es decir, saber aplicar el PRIMER CASO DE
FACTORIZACION.
FACTOR COMÚN EN GRUPOS / EXPLICACIÓN
DEL EJEMPLO 2
EJEMPLO
2: (Con términos negativos
y "Resultado desordenado")
4a - 4b - xb
+ xa =
4. (a - b) +
x. (- b + a) =
4. (a - b) +
x. (a - b) =
(a - b).(4 +
x)
En el primer paso quedó desordenado,
pero luego cambio el orden de los términos, ya que (- b + a) es igual que (a -
b)
EXPLICACIÓN:
PASO
1: Agrupación de a
dos términos
Agrupo 4a con 4b (ya que entre hay
factor común "4" entre ellos) y, por otro lado xb con xa (ya que hay
factor común "x" entre ellos).
Al sacar factor común 4 en los
primeros dos términos, queda 4.(a - b)
Al sacar factor común x en los dos
últimos términos, queda x.(-b + a)
4. (a - b) + x. (-b + a) (para saber por qué el signo +,
consultar en el EJEMPLO 1)
PASO
2: Ordenar los términos
Los resultados de sacar factor común
en las dos agrupaciones son iguales, aunque no lo parezca a simple vista:
(a - b) es lo mismo que (-b + a). Se
trata de las mismas letras, con el mismo signo cada una, pero en otro orden.
Analicemos cada uno:
En (a - b), la "a" es
"positiva", y la "b" es "negativa" (¿por qué la "a" es
"positiva"?)
En (-b + a), la "a es
"positiva", y la "b" es "negativa"
(más explicación sobre estos
"análisis")
Si invierto en orden en (-b + a), me
queda (+a - b), que es lo mismo que (a - b), ya que el "+" adelante
de la "a" no se pone (¿por qué no se pone el "+"?)
Entonces, como (-b + a) es igual que
(a -b), puedo reemplazarlo, y queda:
4. (a - b) + x. (a - b)
PASO
3: Sacar Factor Común
(a - b)
Llegamos entonces a la situación
normal, vista ya en el PASO 2 de los Ejemplos 1 ó 3. Podemos sacar factor común
(a - b)
(a - b).(4 + x)
EJEMPLO
3: (Agrupando términos no consecutivos)
No siempre se puede agrupar en el
orden en que viene el ejercicio. Tiene que haber factor común entre los que
agrupamos, y el "resultado" debe dar igual En este caso tuve que agrupar primero
con tercero y segundo con cuarto.
EXPLICACIÓN:
PASO
1:
Agrupo 4x2a con 12ax (ya que entre hay
factor común "4ax" entre ellos) y, por otro lado agrupo 3y con yx (ya
que hay factor común "y" entre ellos).
Al sacar factor común "4ax"
en 1er y 3er término, queda 4ax. (x + 3)
Al sacar factor común "y" en
los otros dos términos, queda y. (3 + x)
4ax. (x + 3) + y. (3 + x) =
PASO
2:
Los resultados de sacar factor común
son iguales pero "desordenados", como ya vimos en ejemplos anteriores
(¿desordenados?). Entonces, en este paso ordeno el segundo término. Es decir,
pongo (x + 3) en vez de (3 + x):
4ax. (x + 3) + y. (x + 3) =
PASO
3:
Ahora sí se ven iguales los
resultados. No queda más que sacar (x + 3) como factor común:
(x + 3). (4ax + y)
_________________________________________________________________________
x2 + 6x + 9 = (x + 3)2
x 3
2.3.x
6x
CASO III
TRINOMIO CUADRADO PERFECTO / EJERCICIOS RESUELTOS
EJEMPLO 1: (Términos positivos)
x2 + 6x + 9 = (x + 3)2
x 3
2.3.x
6x
Busco dos términos que sean "cuadrado" de algo. Son: x2 y
9. Entonces "bajo" la x y el 3 (las bases). Luego verifico 2.x.3 = 6x
("doble producto del primero por el segundo"). Dió igual que el otro
término. El polinomio es un cuadrado "perfecto". El resultado de la
factorización es la suma de las bases elevada al cuadrado: (x + 3)2 .
EJEMPLO 2: (Con el "1")
x2 + 2x + 1 = (x + 1)2
x 1
2.1.x
2x
Recordemos
que el "1" es cuadrado (de "1" y "-1"). Las bases
son: x y 1. La verificación de que es "perfecto" es 2.x.1 = 2x. El
resultado es (x + 1)2.
EJEMPLO
3: (Con fracciones)
La fracción 16/9 es cuadrado de 4/3. Las bases son x y 4/3.
x2 + 8/3 x + 16/9 = (x + 4/3)2
x 4/3
2. 4/3 . x
8/3 x
La fracción 16/9 es cuadrado de 4/3. Las bases son x y 4/3.
EJEMPLO
4: (Con un término negativo)
_________________________________________________________________________________
x3 + 6x2 + 12x + 8 = (x + 2)3
x 2
3.x2.2 3.x.22
6x2 12x
_________________________________________________________________________________
EXPLICACIÓN:
A- POR EL MÉTODO DE LA DIVISIÓN:
| 1 0 0 -8
|
|
2| 2 4 8
1 2 4 |0
El cociente es entonces: x2 + 2x + 4. Y el resto es 0, como debe ser.
4) Pongo el polinomio por el que dividí: (x - 2), multiplicando al cociente de la división:
EJEMPLO 2: (Suma de Potencias Impares)
x5 + 32 = (x + 2).(x4 - 2x3 + 4x2 - 8x + 16)
x 2
| 1 0 0 0 0 32
|
|
-2| -2 4 -8 16 -32
1 -2 4 -8 16 |0
Cociente: x4 - 2x3 + 4x2 - 8x + 16
x2 - 10x + 25 = (x
- 5)2
x
(-5)
2.(-5).x
-10x
Tomo como bases a "x" y "(-5)", ya que (-5)2 también
es 25. Y con (-5), la verificación del doble producto dá bien. El resultado es
la suma de las bases, al cuadrado. O sea (x + (-5))2 , que es
igual a (x - 5)2.
_________________________________________________________________________________
CASO IV
CUATRINOMIO CUBO PERFECTO /
EJERCICIOS RESUELTOS
EJEMPLO
1: (Todos los términos son positivos)
x3 + 6x2 + 12x + 8 = (x + 2)3
x 2
3.x2.2 3.x.22
6x2 12x
Las bases son x y 2.
Los dos "triple-productos" dan bien (6x2 y 12x). El resultado de la factorización es "la suma de las bases, elevada al
cubo".
EJEMPLO
2: (Con términos negativos)
x3 - 9x2
+ 27x - 27 = (x - 3)3
x -3
3.x2.(-3) 3.x.(-3)2
-9x2
27x
Las bases son x y -3, ya que (-3)3 es igual a -27. Y los dos
"triple-productos" dan bien. El resultado es (x + (-3))3, que es igual a (x - 3)3
EJEMPLO
3: (Con todos los términos negativos)
DIFERENCIA
DE CUADRADOS / EJERCICIOS RESUELTOS
-x3 - 75x
- 15x2 - 125 = (-x
- 5)3
-x
-5
3.(-x)2.(-5)
3.(-x).(-5)2
-15x2
-75x
Las bases son -x y -5, ya que (-x)3 es igual a -x3,
y (-5)3 es igual a -125. Los dos "triple-productos"
dan con los signos correctos. El resultado es (-x + (-5))3, que es
igual a (-x -5)3.
EJEMPLO
4: (Con fracciones)
Las bases son x y 1/2, ya que (1/2)3 es igual a 1/8.
_________________________________________________________________________________
x3 + 3/2 x2
+ 3/4 x + 1/8 = (x + 1/2)3
x 1/2
3.x2.
1/2 3.x.(1/2)2
3/2 x2
3/4 x
Las bases son x y 1/2, ya que (1/2)3 es igual a 1/8.
_________________________________________________________________________________
CASO V
DIFERENCIA
DE CUADRADOS / EJERCICIOS RESUELTOS
EJEMPLO
1:
x2 - 9 = (x + 3).(x - 3)
x 3
Los dos términos son cuadrados. Las "bases" son x y 3. Se factoriza
multiplicando la
"suma de las bases" por la "resta de las
bases".
EJEMPLO 2:
x2 - y2 = (x + y).(x - y)
x y
Las dos bases son letras EJEMPLO 3:
b2 - 1 = (b + 1).(b - 1)
b 1
No hay que olvidar que el número 1 es un cuadrado. |
|
EJEMPLO 4: (Con fracciones)
x2 - 9/25 = (x + 3/5).(x - 3/5)
x 3/5
9/25 es cuadrado. Porque 9 es cuadrado (de 3), y 25 también (de 5) EJEMPLO 5: (Con potencias distintas de 2)
x6 - 4 = (x3 + 2).(x3 -
2)
x3 2
x6 es también un cuadrado, es el cuadrado de x3. Ya que (x3)2 es igual a x6 |
|
CASO VI
SUMA O RESTA DE POTENCIAS DE IGUAL GRADO / EJERCICIOS RESUELTOS
EJEMPLO 1: (Resta de Potencias Impares)
x3 - 8 = (x
- 2).(x2 +
2x + 4)
x 2
Cuando es una resta de
potencias impares, hay que dividir por la resta de las bases.
EXPLICACIÓN:
A- POR EL MÉTODO DE LA DIVISIÓN:
1) x3 es potencia tercera. Entonces, averiguo si 8 es
también potencia tercera de algún número. Calculo la raíz tercera de 8, que es
igual a 2. O pienso: "¿Hay algún número elevado a la 3 me dá 8?", y
me doy cuenta que el número 2 cumple con eso, ya que 23 =
2.2.2 = 8.
2) "Bajo las bases", que son x y 2. Ya que son las que,
elevadas a la tercera, dan x3 y
8.
3) Divido el polinomio (x3 - 8) por el polinomio (x - 2). Porque en la RESTA de
potencias IMPARES, debo dividir por la RESTA de las bases. Es decir: RESTA SE
DIVIDE POR RESTA. Utilizo el método de Ruffini:
| 1 0 0 -8
|
|
2| 2 4 8
1 2 4 |0
El cociente es entonces: x2 + 2x + 4. Y el resto es 0, como debe ser.
4) Pongo el polinomio por el que dividí: (x - 2), multiplicando al cociente de la división:
(x2 + 2x + 4). Así, queda factorizado x3 -
8:
(x - 2).( x2 + 2x + 4)
Ya que DIVIDENDO = DIVISOR POR COCIENTE
(x - 2).( x2 + 2x + 4)
Ya que DIVIDENDO = DIVISOR POR COCIENTE
POR LA REGLA PARA HALLAR EL COCIENTE SIN HACER LA DIVISIÓN:
Para quienes lo ven de esta otra forma, explico los pasos a seguir en este
ejemplo (y en todos los demás).
1) El primer paso es igual que con el otro método: x3 es
potencia tercera. Entonces, averiguo si 8 es también potencia tercera de algún
número. Calculo la raíz tercera de 8, que es igual a 2. O pienso: "¿Hay
algún número elevado a la 3 me dá 8?", y me doy cuenta que el número 2
cumple con eso, ya que
23 = 2.2.2 = 8.
2) Por ser x3 - 8 una RESTA de potencias IMPARES, tengo que usar la
RESTA de la BASES, que son x y 2 Voy "armando" el resultado:
x3 - 8 = (x - 2).(...............)
3) Y ahora, para completar lo que falta, empiezo con x2 y
el 20. Es decir, con las bases elevadas al exponente más alto
("2", uno menos que el polinomio a factorizar), y el exponente más
bajo (cero). Y luego voy bajando el exponente de x en los siguientes términos,
mientras que subo el exponente del 2. Los términos irán todos positivos, porque
así dice la regla que deben ser cuando se factoriza una RESTA. Me queda así:
x3 - 8 = (x - 2).(x2.20 + x1.21 + x0.22)
4) Por último, resuelvo las potencias y multiplicaciones para llegar a la
expresión más simple:
x3 - 8 = (x - 2).(x2.1 + x.2 + 1.4 )
= (x - 2).(x2 + 2x + 4)
EJEMPLO 2: (Suma de Potencias Impares)
x5 + 32 = (x + 2).(x4 - 2x3 + 4x2 - 8x + 16)
x 2
| 1 0 0 0 0 32
|
|
-2| -2 4 -8 16 -32
1 -2 4 -8 16 |0
Cociente: x4 - 2x3 + 4x2 - 8x + 16
Los dos términos son potencias quintas. Ya que
32 = 25.
Cuando es una suma de potencias impares, hay que dividir al polinomio por la
suma de las bases:
(x + 2). Y la división se suele hacer con la regla de
Ruffini.
Divido (x5 + 32):(x +
2), y el resultado de la división es: x4 - 2x3 + 4x2 - 8x + 16. El resto dá 0. Se factoriza
como (x + 2).(x4 - 2x3 + 4x2 - 8x + 16), es decir: "la suma de
las bases multiplicada por el resultado de la división".
Pero también hay otra forma de factorizar este tipo de polinomio, que consiste
en aplicar una reglita para construir el cociente sin hacer ninguna división.
En cada ejemplo, se dá la explicación para hacerlo de las dos maneras.
La variedad de los siguientes ejemplos está pensada para las distintas
situaciones que se presentan al utilizar el método de la división con la regla
de Ruffini. Con el método de la regla, casi no hay variedad de situaciones:
todos los ejercicios resultan prácticamente iguales.
_________________________________________________________________________________
CASO VII
TRINOMIO DE SEGUNDO GRADO" / EJERCICIOS RESUELTOS
EJEMPLO
1: (Un primer ejemplo)
x2 + 3x + 2 = (x + 1).(x + 2)
x1,2 = 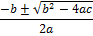
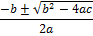
a = 1
b = 3
c = 2
x1,2 = 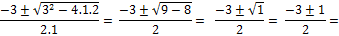
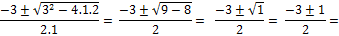
x1 = 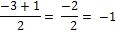 (con
la suma)
(con
la suma)
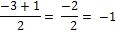 (con
la suma)
(con
la suma)
x2 = 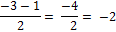 (con
la resta)
(con
la resta)
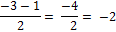 (con
la resta)
(con
la resta)
x1 = -1
x2 = -2
a. (x - x1).(x - x2) = (x - (-1)).(x - (-2)) = (x
+ 1).(x + 2)
Es un "trinomio", pero no es "cuadrado perfecto". Se puede factorizar
buscando las "raíces" con la fórmula para resolver ecuaciones
cuadráticas. Y se factoriza así: a.(x - x1).(x - x2). En
este ejemplo "a" es igual 1, entonces no lo ponemos. También hay otro
método para factorizarlo, pero no se puede aplicar en cualquier ejemplo.
EJEMPLO
2: (Con coeficiente principal distinto de
"1")
2x2 - 3x + 1 = 2.(x - 1).(x - 1/2)
En este ejemplo, el coeficiente principal es 2. No hay que olvidarse de ponerlo
en la factorización.
EJEMPLO 3: (Con fracciones)
1/3 x2 - 1/3 x - 2 = 1/3. (x - 3).(x + 2)
Los coeficientes son fracciones. Eso puede complicar un poco el cálculo de las
raíces.
EJEMPLO
4: ("No tiene solución en Reales")
x2 - 6x + 10 = No se factoriza
Cuando aplico la "fórmula de la cuadrática", queda una raíz cuadrada de un número negativo, que no tiene solución en el Conjunto de los Números Reales. Entonces un ejemplo así no se factoriza.
x2 - 6x + 10 = No se factoriza
Cuando aplico la "fórmula de la cuadrática", queda una raíz cuadrada de un número negativo, que no tiene solución en el Conjunto de los Números Reales. Entonces un ejemplo así no se factoriza.
Para mayor información visite la pagina:
http://matematicaylisto.webcindario.com/polinomios/factoreo/factoreo.htm





0 comentarios: